Correction des graphes

J'ai corrigé vos laboratoires en utilisant ce programme. Le programme réalise les opérations suivantes:

• Crée un graphe à 11 sommets
• Définit le sommet de départ comme étant le sommet 0
• Tente d'enlever une arête en lui passant des entiers (ceci ne doit pas planter même s'il n'y a encore aucune arête dans le graphe)
• Tente d'enlever une arête en lui passant une arête (même commentaire)
• Ajoute tout un tas d'arêtes en passant des entiers
• Ajoute une arête en lui passant une arête
• Enlève une arête existante par entiers
• Enlève une arête existante par arête
• Affiche tous les sommets du graphe et, pour chacun d'eux, tous ses voisins avec la distance qui les sépare, en utilisant les itérateurs
• Appelle Dijkstra avec le sommet 10 comme fin.
• Utilise la méthode montrée dans l'énoncé pour retrouver le chemin le plus court de 0 à 10, une fois que Dijkstra a préparé le graphe.
• Réinitialise le graphe en le réinstanciant et en ajoutant de nouveaux toutes les arêtes (par entiers)
• Appelle Dijkstra sans sommet de fin
• Utilise la méthode montrée dans l'énoncé pour retrouver le chemin le plus court de 0 à 9 (j'aurais pu prendre n'importe quel autre mais j'ai choisi celui-ci)

Le graphe qui est créé par le programme est le suivant:

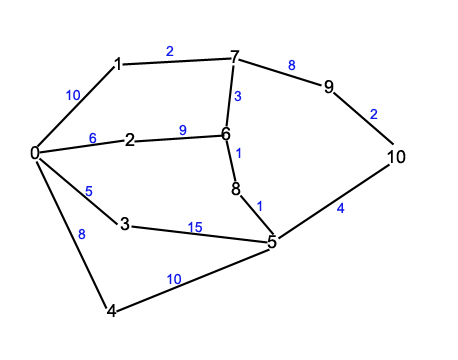
Le meilleur chemin de 0 à 10 est 0-2-6-8-5-10 (coût 21). Il y a aussi un chemin équivalent (merci au programme de Jonathan Roy pour l'avoir remarqué!): 0-1-7-6-8-5-10 (lui aussi à coût 21).

Le meilleur chemin de 0 à 9 est 0-1-7-9 (coût 20).

Etienne Forest, 18 décembre 2007